Soit C un point d'un cercle de centre O et de diamètre [AB]. Soit D le symétrique de A par rapport à C. Soit E l'image de D par la translation de vecteur OA.
1) Démontrer que C est le milieu de [OE].
2) Démontrer que : (OE)//(BD).
Soit C un cercle de centre O et de rayon 4 cm. Soit O' tel que OO' = 6cm. Soit C' l'image du cercle C par la translation T de vecteur OO'. Ces deux cercles se coupent en A et en B. Soit B' l'image de B par la translation T.
1) Montrer que : (AB) est perpendiculaire à (OO')
2) Montrer que : (AB) est perpendiculaire à (BB')
3) Montrer que : B' appartient à C'.
4) Montrer que [AB'] est un diamètre de C'.
ABC est un triangle équilatéral. Soit J le milieu de [BC]. Soient E et F les symétriques respectifs de J et de A par rapport à B.
Démontrer que BEF et CAF sont des triangles rectangles.
Soit ABC un triangle quelconque. Soient M et P les milieux respectifs de [AB] et de [AC]. Soit Q le symétrique de M par rapport à P. Les droites (AQ) et (BC) se coupent en D.
1) Quelle est la nature du quadrilatère MAQC ?
2) Montrer que C est le milieu de [BD] et que Q est le milieu de [AD].
Soit ABC un triangle acutangle, d'orthocentre H. Soient K le pied de la hauteur issue de A et O le centre du cercle (c) circonscrit à ABC. Soit D le point diamétralement opposé à A sur (c).
1) Que peut-on dire des triangles ABD et ACD ?
2) Quelle est la nature du quadrilatère HCDB ?Montrer que [HD] et [BC] se coupent au milieu I de [BC].
3) Soit H' le point d'intersection du cercle circonscrit et de (AH). Montrer que H' est le symétrique de H par rapport à (BC).
|
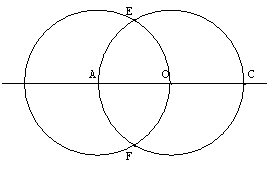
± 1) Donner un programme de construction de la figure ci-contre (les cercles sont de même rayon). 2) Quels sont les axes de symétrie de la figure ? 3) On complète la figure en traçant le carré ABCD tel que B soit du même côté de (AC) que E. Soit G l'intersection des droites (AB) et (CE), soit H l'intersection des droites (AD) et (CF). Montrer que G et H sont symétriques par rapport à la droite (AC). 4) Montrer que le triangle CGH est équilatéral. |
 |
Soit ABCD un parallélogramme. On désigne par I, J, K, L les projetés orthogonaux, respectivement de A sur (BD), de B sur (AC), de C sur (BD) et de D sur (AC). Quelle est la nature du quadrilatère IJKL ?
Soient C et C' deux cercles de même rayon r, tangents en un point T. Soient (d) et (d') deux droites perpendiculaires, sécantes en T. (d) recoupe C en M et C' en P, (d') recoupe C en Q et C' en N.
Quelle est la nature du quadrilatère MNPQ ?
Soit C un cercle de centre O et de rayon r, soit un point P extérieur à ce cercle. On mène les deux tangentes à C passant par P. Soient A et B les deux points de tangence.
1. Montrer que les triangles PAO et POB sont isométriques.
2. Montrer que la droite (OP) est bissectrice de l’angle AOB et
médiatrice du segment [AB].
C et C' sont deux cercles de même centre O. deux droites d et d’, passant par O, coupent C respectivement en M et N et C' respectivement en U et V.
Montrer que UN=VM.
Dans un cercle, les cordes [AB] et [CD] sont de même longueur. [BC] et [AD] sont sécantes en un point E.
Montrer que les triangles EAB et ECD sont isométriques.
En déduire que (OE) est la médiatrice de [BD]
ABC est un triangle isocèle rectangle en A et I est le milieu du segment [BC].
On choisit un point P quelconque sur l’hypoténuse et on construit M sur [AB] et N sur [AC] afin que AMPN soit un rectangle.
1. Quelle est la nature du triangle MNI ? (On pourra utiliser un quart de tour de centre I)
2. Montrer que les points A,N,I,P,M appartiennent à un même cercle dont on précisera le centre.
3. Montrer que les angles INP et PMI ont la même mesure.
Soit ABC un triangle équilatéral. On définit les
points K, S et L par :
vec(AK) = 1/3 vec(AB)
vec(BS ) = 1/3 vec(BC)
vec(CL) = 1/3 vec(CA)
Soient respectivement M le point d’intersection de [AS] et de [CK], N le point
d’intersection de [AS] et de [BL], P le point d’intersection de [BL] et de [CK].
Montrer que le triangle MNP est équilatéral.
|
Soient (D) et (D’) deux droites sécantes. A tout point M du plan on associe le point M’ vérifiant les conditions suivantes :
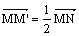Construire l’image du polygone par l’affinité précédemment décrite. |
 |
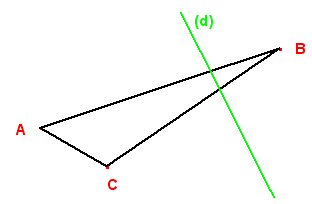
| Construire, à la règle non graduée et au compas seuls et en justifiant, l’image du triangle ABC par la symétrie d’axe (d). |  |
 |
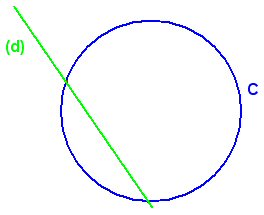Construire, à la règle non graduée et au compas seuls et en justifiant, l’image du cercle C par la symétrie d’axe (d).
|
|
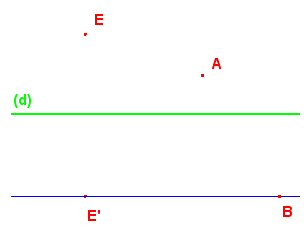
Le seul instrument autorisé est une règle non graduée. E’ est le symétrique de E par rapport à (d). 1. Construire le symétrique de A par rapport à (d) en justifiant. 2. B est un point tel que (BE’) est parallèle à (d). Construire le symétrique B’ de B par rapport à (d). |
 |
Construire à la règle non graduée seule, le symétrique de A par rapport à O, où A est intérieur au cercle de centre O.
Construire, à la règle non graduée seule et en justifiant, l’axe de symétrie d’un trapèze isocèle ABCD de bases [AB] et [CD].
On considère un parallélogramme ABCD et un cercle de même centre O et de diamètre [AC].
Quelle est l’image de la droite (AB) par la symétrie centrale sO de centre O ?
Quelle est l’image du cercle par la symétrie sO ?
Quelle est l’image du point N par la symétrie sO ?
En déduire la nature du quadrilatère AMCN.
|
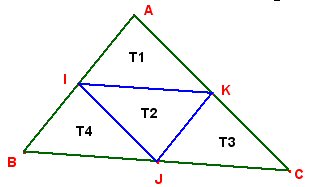
ABC est un triangle quelconque. Les points I, J et K sont les milieux respectifs des côtés [AB], [BC} et [AC]. 1. Par quelle transformation, le triangle T1 a-t-il pour image le triangle T3 ? le triangle T2 ? le triangle T4 ? 2. Justifier que les quatre triangles T1, T2, T3, T4 ont la même aire Д puis que l’aire du triangle ABC est égale à 4pi |
 |
|
L’image du point A ci-contre par une symétrie centrale est A’. Tracez le symétrique B’ de B par cette même symétrie.
|
 |
|
Soient deux triangles OAB et OCD rectangles isocèles en O.
|
 |
On donne deux droites (d) et (d’) distinctes.
1. Y a-t-il des translations qui transforment (d) en (d’) ? Si oui, en déterminer une.
2. Y a-t-il des symétries axiales qui transforment (d) en (d’) ? Si oui, en déterminer une.
3. Y a-t-il des symétries centrales qui transforment (d) en (d’) ? Si oui, en déterminer une.
4. Y a-t-il des rotations qui transforment (d) en (d’) ? Si oui, en déterminer une.
ABCD est un carré de centre O. Soit E un point du segment [BC] et F un point du segment [CD] tel que BE = CF.
On considère la rotation de centre O et d’angle – 90°.
1. Démontrez que l’image du triangle ABE par cette rotation est le triangle BCF.
2. Démontrez que les droites (AE) et (BF) sont perpendiculaires.
1. Construisez un triangle équilatéral ABC.
2. Construisez
le point D tel que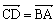 
3. Construisez le point G, image de B par la rotation de centre A qui transforme C en B
4. Construisez le point E symétrique du point B par la symétrie centrale de centre A.
5. Construisez le point F, image du point E par la translation qui transforme C en B.
6. Quelle conjecture peut-on faire quant à la nature du polygone BCDEFG ?
ABC est un triangle isocèle rectangle en A. Le point I est le milieu du segment [BC]. Soient B’ et C’ les points extérieurs au triangle ABC tels que les triangles AC’B et AB’C sont équilatéraux.
K est le point d’intersection des droites (BB’) et (CC’), L est celui des droites (BC’) et (B’C).
1. Démontrez que le point B’ est l’image du point C’ par la symétrie orthogonale d’axe (AI).
2. Par cette même symétrie, quelles sont les images des droites (CC’) et (C’L) ?
3. En déduire que les points A, K, I et L sont alignés.
Soient (d) une droite du plan, A et B deux points du plan n’appartenant pas à cette droite.
Construisez le point M de la droite (d) tel que la longueur MA + MB soit la plus petite possible dans les deux cas suivants :
1. les points A et B sont de part et d’autre de la droite (d) ;
2. les points A et B sont d’un même côté de la droite (d).
Déterminez et tracez le(s) axe(s) de symétrie et centre(s) de symétrie(s) des figures usuelles : segment, triangle isocèle, triangle équilatéral, parallélogramme, carré.
Soit h l’homothétie de centre O et de rapport 2,5. Construisez l’image de la droite (d) par h.
|
Soient C et C1 deux cercles de centres respectifs O et O1. Soit I un point de C. Construisez les cercles images de C et C1 par l’homothétie h de centre I et de rapport ½ en justifiant.
|
 |
|
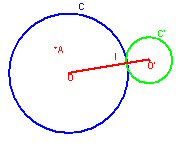
± C et C’ sont deux cercles tangents en I. Construisez, à la règle non graduée seule et en justifiant, l’image de A par l’homothétie de centre I qui transforme O en O’. |
 |
|
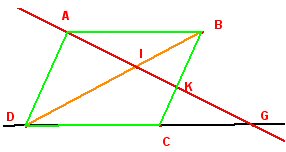
ABCD est un parallélogramme, I un point quelconque du segment [BD], distinct de B et de D. La droite (AI) coupe la droite (BC) en K et la droite (DC) en G. Trouvez toutes les paires de triangles homothétiques de la figure en justifiant brièvement. |
 |
