 |
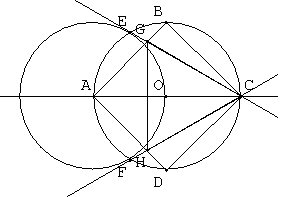
1) Choisir deux points A et O. Tracer le cercle de centre A et de rayon AO, puis le cercle de centre O et de même rayon, ces deux cercles se coupent en E et F. Tracer la droite (AO). Cette droite coupe le second cercle en C. 2) Les axes de symétrie de la figure sont (AO) et (EF). 3) (AB) et (AD) sont symétriques par rapport à (AO) car (AO) est un axe de symétrie du carré. E et F sont symétriques par rapport à (AO), donc (CE) et (CF) sont également symétriques. L'intersection de (CE) et (AB) est donc symétrique de l'intersection de (CF) et (AD), c'est à dire G et H. 4) CG=CH d'après la question précédente. Le triangle est équilatéral, donc l'angle OAE mesure 60°. Le triangle AEC est rectangle car [AC] est un diamètre. Donc l'angle ACG mesure 30°. Donc l'angle mesure 60°. Donc le triangle GHC est équilatéral.
|