 |
1)
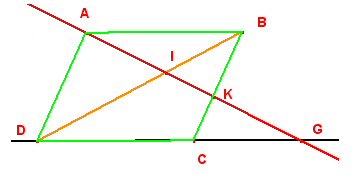
ABCD est un
parallélogramme et les droites (CD) et (DG) sont confondues : les
droites (AB) et (DG) sont donc parallèles. Les points A, I, G et B, I, D
sont alignés dans le même ordre. Les triangles AIB et DIC forment une
configuration de Thalès (configuration du sablier ou du papillon) : ils
sont donc homothétiques. L’homothétie transformant AIB en IDG est de
centre I et de rapport k négatif, tel que |k|= ABCD étant un parallélogramme, les droites (BC) et (AD) sont parallèles ; les points G, C, D et G, K, A sont alignés dans le même ordre (configuration classique de Thalès). Il existe une homothétie de centre G, transformant le triangle GCK en le triangle GDA et de rapport l positif, l vérifiant : l = Les droites (BK) et
(AD) sont parallèles, les points K, I, A et B, I, D sont alignés dans le
même ordre : on peut donc appliquer la propriété de Thalès aux triangles
BIK et AID (configuration du papillon). Ces deux triangles sont donc
homothétiques : l’homothétie qui transforme le triangle BIK en le
triangle DIA est de centre I et de rapport m négatif, m vérifiant : m =
|