 |
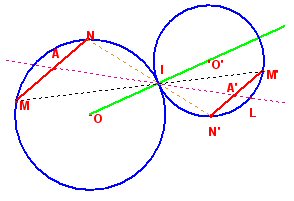
1) Comme les deux cercles sont tangents en I, C’ est l’image de C par l’homothétie H de centre I et de rapport - IO’/IO (rapport négatif étant donné que le point O’ ne se situe pas sur la demi-droite [IO)). Notons A’ l’image de A par H et L l’intersection de la droite (AI) avec le cercle C’. A’ se situe sur la demi-droite [IL). Soient M et N deux points du cercle C tel que A appartienne à la corde [MN] ; notons M’ et N’ leurs images par H. M est l’intersection du cercle C et de la droite (IM) (invariante par H) ; son image M’ est l’intersection du cercle C’ et de la droite (IM). De même, N’ est l’intersection du cercle C’ et de la droite (IN). A est l’intersection des droites( IL) et (MN) : son image A’ est alors l’intersection des droites (IL) et (M’N’).
|