 |
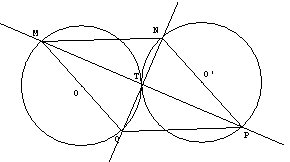
1) Le point T est centre de symétrie des deux cercles et des deux droites (d) et (d'). Les points M et P, d'une part, N et Q d'autre part sont symétriques par rapport à T. MNPQ est donc un parallélogramme. De plus les diagonales sont perpendiculaires, donc MNPQ est un losange. Dans une configuration particulière, MNPQ peut être un carré. Il faut pour cela qu'il y ait quatre axes de symétrie, donc que les droites (d) et (d') soient symétriques par rapport à (OO').
|