 |
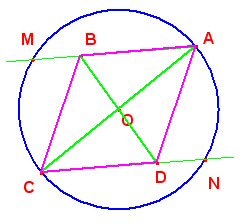
1) ABCD est un parallélogramme ; notons SO la symétrie de centre 0. 1. O étant centre du parallélogramme, la symétrie SO transforme B en D et A en C. La droite (AB) est donc transformée en la droite (CD). 2. Comme le cercle est de centre O, il est (globalement) invariant par SO. 3. Le point N est l’intersection du cercle (C) et de la droite (DC) ; son image par SO est donc l’intersection des images de (C) et de (CD) par SO, autrement dit l’intersection de (C) et de la droite (AB), autrement dit le point M. 4. Comme la symétrie centrale est une isométrie, le segment [CN] est transformé en un segment de même longueur, en l’occurrence le segment [AM] ; de plus l’image de la droite (CN) est une droite qui lui est parallèle : ainsi les droites (CN) et (AM) sont parallèles. Finalement, le quadrilatère AMCN a deux côtés parallèles et de même longueur : c’est un parallélogramme.
|