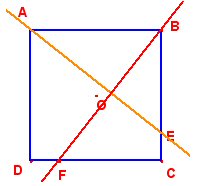
1)    Notons R la rotation de centre O et d’angle – 90°.

1.      ABCD est un carré de centre O ; ses diagonales sont perpendiculaires, de même longueur et se coupent en leur milieu O. Ainsi l’image de A par R est B, celle B est C, celle de C est D qui a pour image A par R.

Le point E appartient au segment [BC] ; son image E’ sera sur l’image du segment [BC] par R, car la rotation conserve l’alignement. E’ est donc sur le segment [CD].

De plus E’ sera sur le segment [CD], vérifiant CE’ = BE, car la rotation conserve les longueurs. Le seul point vérifiant ces conditions est le point F : ainsi F est l’image de E par R. On peut affirmer que le triangle ABE est transformé en triangle BCF par R.

2.      La droite (AE) est transformée en la droite (BF). Elles sont sécantes en un point I, en formant deux angles supplémentaires, l’un d’eux mesurant 180 – (valeur absolue de l’angle de rotation). Comme la rotation est d’angle – 90°, un angle mesurera 90° (et donc l’autre également). Ainsi les droites (AE) et (BF) sont perpendiculaires.

2

Démonstration de la propriété utilisée ci-dessus

On raisonne en angles non orientés

Soient (d) une droite, O un point non situé sur cette droite et un angle a de mesure différente d’un multiple de 180°.

On considère la rotation de centre O et d’angle a.

Comme l’angle n’est pas plat, la droite et son image (d’) ne sont pas parallèles ; elles se coupent en un point noté I.

Pour simplifier, on considère le projeté orthogonal M de O sur (d), d’image M’ sur (d’) par cette rotation. La droite (OM) étant perpendiculaire à (d), son image (OM’) est perpendiculaire à (d’), car une rotation conserve les angles. Les distances OM et OM’ sont égales car une rotation conserve les longueurs. Ainsi le point O est équidistant des droites (d) et (d’), c'est-à-dire qu’il appartient à la bissectrice de l’angle MIM’ (autrement dit, la droite (IO) est bissectrice de l’angle MIM’). Dans le triangle IMO, rectangle en O, l’angle IOM mesure a/2, ce qui permet d’affirmer que l’angle MIO mesure 90 – a/2. L’angle MIM’ mesurant le double de l’angle précédent, il mesure donc 180 – a. L’angle supplémentaire mesurera donc a.

Retour aux exercices