 |
|
|
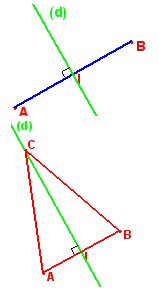
Le segment [AB] est symétrique par rapport :
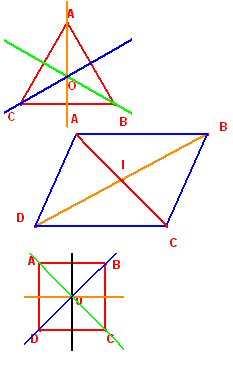
Triangle ABC, isocèle de sommet principal C L’unique axe de symétrie de la figure est la médiatrice principale, i.e. la médiatrice du segment de base [AB]. Le triangle ne présente pas de centre de symétrie. Triangle équilatéral ABC Il présente trois axes de symétrie qui sont les médiatrices des trois côtés. Pas de centre de symétrie. Les rotations de centre O et d’angle des multiples de 120° laissent le triangle équilatéral globalement invariant. Parallélogramme ABCD I, intersection des diagonales du parallélogramme, est centre de symétrie (puisque les diagonales se coupent en leur milieu). Carré ABCD Le carré possède quatre axes de symétrie (les diagonales et les médiatrices de deux côtés consécutifs), et un centre de symétrie O, intersection des diagonales. On peut rajouter que les rotations de centre 0 et d’angles des multiples de 90°, laissent le carré globalement invariant.
|
|