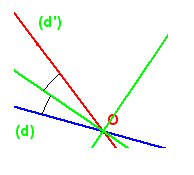
Si (d) et (d’) sont sécantes en un point O

Il n’existe pas de translation de vecteur non nul permettant de passer de (d) à (d’), car elle ont un point commun.

Il existe deux symétries axiales transformant (d) en (d’) ; les axes sont les bissectrices (perpendiculaires) des angles formés par les droites (d) et (d’).

Il n’existe pas de symétrie centrale transformant (d) en (d’) car l’image d’une droite par une symétrie centrale est une droite lui étant parallèle.

Il existe deux rotations transformant (d) en (d’) ; elles sont toutes les deux de centre O, mais d’angles a et 180 – a.

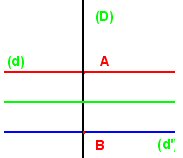
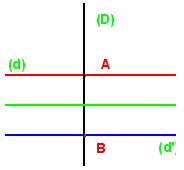
Si (d) et (d’) sont strictement parallèles

Soient A un point de (d) et B un point de (d’). La translation de vecteur  transforme (d) en (d’) : tout couple de points (A ; B) convient (l’image d’une droite par une translation étant une droite parallèle).

La médiatrice du segment [AB] est axe de symétrie de la figure ; la symétrie par rapport à cette droite transforme (d) en (d’) et réciproquement.

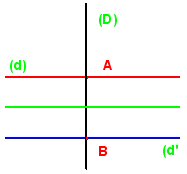Tout point de la médiatrice du segment [AB] est centre de symétrie de la figure.

Il existe une infinité de rotations permettant de transformer (d) en (d’) : elles sont toutes d’angle 180° et de centre un point de la médiatrice du segment [AB].