|
1)
1.
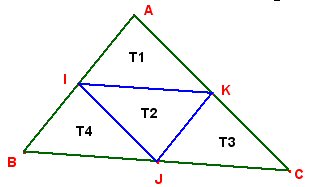
Comme K est milieu de [AC], on a
 .
De plus, comme I et J sont les milieux resp. des segments [AB] et [BC],
on montre par la propriété de la droite des milieux que le segment [IJ]
a même longueur que le segment [KC] et que les droites (IJ) et (AC) sont
parallèles ; on conclut que  .
On peut donc affirmer que le triangle T3 est l’image du triangle T1 par
la translation de vecteur .
Un
raisonnement analogue permet de montrer que le triangle T4 est l’image
du triangle T1 par la translation de vecteur
 .
Comme  ,
le quadrilatère AKJI est un parallélogramme : les triangles T1 et T2
sont alors symétriques l’un de l’autre par rapport au milieu du segment
[IK].
2.
Les transformations du plan précédemment citées étant des
isométries, les triangles T1, T2, T3 et T4 ont même aire Д. Comme le
triangle ABC est constitué de quatre triangles de même Д, son aire est
le quadruple de pi.
|
