Arithmétique 

retour page d'accueil

Exercice 1

Un nombre de trois chiffres commence par 3 et finit par 4. Le chiffre des dizaines est effacé. Peut-on le retrouver si sait que :

1.  le nombre est divisible par 9 ?

2.  le nombre est divisible par 3 ?

3.  le nombre est divisible par 11 ?

   Solution

Exercice 2

Sachant que 9 531 914 =5 326 x 1 789 + 3 700, donner :

1. le quotient euclidien de 9 531 914 par 5 326.

2. le quotient euclidien de 9 531 914 par 1 789.

Justifier vos réponses.

Solution

Exercice 3

Une caisse a la forme exacte d'un parallélépipède rectangle de dimensions 24 cm, 36 cm et 60 cm. Elle est remplie exactement par des cubes dont l'arète a pour mesure (en cm) un naturel. Combien contient-elle de cubes ?

 

Solution

Exercice 4

Deux horloges ne sont pas bien synchronisées : l'une (A) fait entendre un top par minute, l'autre (B) en fait entendre un toutes les 62 secondes.

1. À midi, on les met en marche en même temps. À quelles heures feront-elles entendre un top en même temps ?

2. Un peu plus d'une heure après leur mise en marche, on voudrait connaître l'heure exacte à une minute près. B fait entendre son top 16 secondes exactement après A. Quelle heure est-il ?

Solution

Exercice 5

Trouver le plus petit nombre entier ayant 21 diviseurs.

 

Solution

Exercice 6

Déterminer tous les nombres N du type 2^p3^q qui possèdent exactement 12 diviseurs.

 

Solution

Exercice 7

On décompte de 3 en 3 à partir de 8932 tant qu'on obtient un entier naturel : "8932, 8929…".

a) Quel nombre termine cette suite ?

b) Combien cette suite de nombres comporte-t-elle de termes ?

c) Quel est le centième terme ? (le premier est 8932)

 

Solution

Exercice 8

Sachant que 8562=34X251+28 et que 18846640=4973X3789+3913,

a) Quels sont le quotient et le reste de la division euclidienne de 8562 par 34 ?

b) Quels sont le quotient et le reste de la division euclidienne de 8532 par 251 ?

c) Quels sont le quotient et le reste de la division euclidienne de 18846640 par 4973 ?

d) Quels sont le quotient et le reste de la division euclidienne de 18846640 par 3789 ?

e) Quels sont le quotient et le reste de la division euclidienne de 85620 par 340 ?

 

Solution

Exercice 9

a) Décomposer 36 en facteurs premiers et justifier que 36 a exactement 9 diviseurs.

b) On note a₁, a₂, a₃…a₉ ces diviseurs, du plus petit au plus grand. Calculer a₁Xa₉, a₂Xa₈, a₃Xa₇, a₄Xa₆. Que constate-t-on ?

c) Peut-on trouver un nombre entier ayant 9 diviseurs dont le produit soit 225⁴X15 ?

 

Solution

Exercice 10

Dans ce problème on va étudier un algorithme permettant d'obtenir des informations sur la divisibilité d'un nombre par 7 sans avoir à effectuer la division.

4 3 2 7 8 9 6 7 4 1 7                                                              7 0 8 3 6 0 5 9

                - 1 7 0                                                                           - 5 9 0

4 3 2 7 8 9 5 0 4                                                                    7 0 7 7 7 0

             - 4 0  

4 3 2 7 8 5 5

    - 5 5 0

4 2 7 2 8

- 2 8 0

  1 4 7

La première partie est destinée à étudier l'algorithme présenté dans deux cas particuliers. L'objectif de la seconde partie est de justifier la conclusion concernant la divisibilité par 7 du nombre initial.

1) a) Dans chacun des deux cas présentés ci-dessus, on s'est arrêté quand on a reconnu que le nombre n était divisible par 7. On en a déduit que le nombre initial l'était aussi. Appliquer l'algorithme à 14 765 432 123 379  et conclure.

    b) Pour le premier exemple, on est passé successivement de 43278967417 à 432789504, puis à 4327855, puis à 42728 puis à 147. Pour le deuxième exemple il a suffi d'une étape pour reconnaître un multiple de 7. D'une manière générale l'algorithme permet, à chaque étape de réduire la longueur du nombre à considérer. Décrire précisément la suite d'actions correspondant à une étape de l'algorithme.

2) a) Soit q le quotient et r le reste de la division euclidienne d'un nombre M par 100. Exprimer, en fonction de q, de r ou des deux :

·        le nombre M.

·        le nombre D constitué des deux derniers chiffres de M.

·        le nombre E obtenu en barrant les deux derniers chiffres de M.

·        le nombre N obtenu en retranchant de E le décuple de D.

b) Démontrer que, si N est un multiple de 7, alors M l'est également.

c) Justifier l'algorithme présenté.

 

Solution

Exercice 11

Combien y a-t-il de multiples de 15 qui sont des nombres à trois chiffres ? Quel est le plus petit ?

        Exercice 12

Dans une corbeille il y a plus de 500 fruits, mais moins de 1000 fruits.

Si on les compte 4 par 4, 5 par 5 ou 6 par 6, il en reste toujours un.

Si on les compte 7 par 7, il n'en reste pas.

Trouver le nombre de fruits dans la corbeille.

Solution

 

Exercice 13

Déterminer les nombres entiers x et y sachant que le quotient de la division euclidienne de x par y est 3, que le reste de cette division est 2 et que la différence entre x et y vaut 38.

Solution

Exercice 14

On prend un nombre de 3 chiffres, par exemple 763, on le réécrit à droite de lui-même pour former un nombre de six chiffres : 763763. On divise le nombre obtenu par 7, puis le quotient obtenu par 11, et le quotient de cette dernière division par 13. Donner le résultat obtenu.

Au vu des résultats précédents, énoncer une proposition générale.

Démontrer cette proposition.

 

Solution

 

Exercice 15

Retrouver les deux chiffres a et b manquant dans le nombre 37a28b pour qu'il soit divisible à la fois par 6 et par 45.

Solution

Exercice 16

On doit conditionner des boîtes parallélépipèdiques de dimensions 6 cm x 18 cm x 23 cm dans des cartons parallélépipèdiques de dimension 140 cm x 95 cm x 62 cm.

Combien de boîtes peut-on conditionner, au maximum, dans chaque carton ?

Solution

Exercice 17

Des cinq chiffres composant le prix de 36 bidules, on ne peut lire que le chiffre des centaines (un 4) et celui des dizaines (un 3). De plus on sait qu'un bidule coûte entre 1100 F et 1450 F.

Donner les prix possibles de 36 bidules (il y a trois solutions)

Heureusement, le petit Jérémy se souvient que le prix d'un bidule est un nombre premier. Donner le prix des 36 bidules. Vérifier que le prix d'un bidule est bien un nombre premier.

Exercice 18

Pour son anniversaire Charlie a eu des chocolats.

-Combien ? demande Bruno.

- Je me rappelle seulement, dit Charlie, qu'il y en avait moins de 100 et que, lorsque je les ai répartis en tas de 2, puis de 3 et enfin de 4, il m'en restait à chaque fois, mais lorsque je les ai répartis en tas de 5, il n'en restait pas.

Combien de chocolats Charlie a-t-il eu pour son anniversaire ?

Solution

Exercice 19

Déterminer tous les entiers naturels compris entre 100 et 200 dont le reste est 8 dans la division euclidienne par 42.

Un nombre x a pour quotient q et pour reste 8 quand on le divise par 42, déterminer le quotient et le reste de la division euclidienne par 42 de ( x + 28), puis de ( x + 40).

Déterminer les entiers naturels y pour lesquels le quotient de la division euclidienne par 42 de x + y est q+1.

Dans la division euclidienne d'un entier naturel x par un entier naturel y, le quotient est 42 et le reste 8.

Quelle est la plus petite valeur possible pour x ?

Déterminer x et y pour que le reste de la division de x + 3 par y soit égal à 0.

 

Solution

Exercice 20

Un nombre a trois chiffres 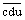, autres que 0.

1.      On permute les chiffres des unités et des centaines. Montrez que 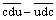 est divisible par 99.

2.      Démontrez que si d = c + u, ce nombre 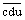 est divisible par 11.

3.      Démontrez que si c + d + u = 9, alors 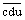 est divisible par 9.   

 

Solution

Exercice 21

Comment doit-on choisir les chiffres x et y pour que :

1.      le nombre A qui s’écrit 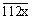soit divisible par 45 ?

2.      le nombre B qui s’écrit 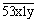soit divisible par 15 ?    

 

Indication

Solution

Exercice 22

Enoncez, pour les nombres qui s’écrivent avec 4 chiffres, un critère de divisibilité par 25 et démontrez-le.

Exercice 23

1.      Le produit pq de deux entiers naturels p et q est impair. Que peut-on dire de la parité de p et de q ?

2.      Le produit pq de deux entiers naturels p et q est pair. Que peut-on dire de la parité de p et de q ?

Exercice 24

Décomposez 2205 en produit de facteurs premiers afin de déterminer le nombre de ses diviseurs.

Quels sont ces diviseurs ?                                                                                                 

Exercice 25

Les nombres 1789 et 2443 sont ils premiers ? Sont-ils premiers entre eux ?                  

Exercice 26

On remarque que 2 et 3 sont deux nombres premiers consécutifs.

Démontrez que si p est un nombre premier supérieur ou égal à 3, alors p + 1 n’est pas premier.

Note : 2 et 3 sont les seuls nombres premiers consécutifs.                                         

Exercice 27

L’affirmation : « Si n est un entier naturel, alors tout nombre entier de la forme n² - n + 11 est toujours un nombre premier »  est-elle vraie ? Justifiez !                                                          

Exercice 28

Calculez, sans utiliser la calculatrice, la racine carrée de 2⁶ ´ 3² ´ 5⁴, puis la racine carrée de 6 084.

Exercice 29

1.      On nomme a, b et c trois nombres entiers multiples de 5 consécutifs. Choisissez plusieurs fois de suite trois       entiers a, b et c et calculer b² - ac.

2.      Quelle conjecture peut-on faire pour le nombre b² - ac ?

3.      Démontrez cette conjecture.

Exercice 30

On veut paver une pièce rectangulaire dont les dimensions sont 12,6 m et 11,2 m, avec un nombre entier de carreaux carrés de même dimension.

Quelle est, en cm, la dimension maximale d (d entier inférieur à 30) du côté d’un carreau ?

Combien de carreaux seront nécessaires ?                                                                                  

Exercice 31

Des photos, toutes de même format (18 cm ´ 24 cm) sont toutes mises bord à bord dans le même sens, recouvrent un panneau carré dont le côté mesure entre 3 et 4 m.

Combien y a-t-il de photos ?                                                                                               

Exercice 32

Déterminez tous les entiers naturels n, compris entre 1 300 et 3 400, tels que

PGCD(n ; 1 380) = 115.