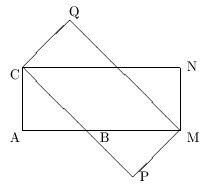
La figure ci-contre a les propriétés suivantes :
|
 |
La figure ci-contre a les propriétés suivantes :
|
|
Reproduire cette figure sur une feuille quadrillée en prenant 4 cm pour mesure de AB (quadrillage 5mm). On tracera [AB] et [AC] sur des lignes du quadrillage). On complétera la figure en utilisant seulement la règle non graduée et le compas, on laissera apparents les trais de construction.
Montrer que les points A, C, Q, N, M et P sont sur un même cercle.
Le polygone ACQNMP est-il un polygone régulier ? On justifiera la réponse.
ABCD est un rectangle tel que AB =8 cm et AD = 6 cm. I et J sont les milieux respectifs des segments [AB] et [CD] ; on désigne par M le point d'intersection de [CI] et de [BD] et par N celui de [AJ] et de [BD].
Construire la figure en utilisant seulement la règle graduée et le compas, en respectant les dimensions données. On laissera apparents les tracés auxiliaires.
Prouver que AICJ est un parallélogramme.
Démontrer que les points M et N partagent le segment [BD] en trois segments de même longueur.
Soit ABCD un carré de côté 6 cm. Tracer les demi-cercles C et C' intérieurs au carré et de diamètres respectifs [AB] et [AD]. Noter I le centre de C, J le centre de C' et A' le point d'intersection de C et de C' situé à l'intérieur du carré.
Déterminer la nature du quadrilatère AIA'J
Calculer l'aire du domaine limité par les arcs de cercle AA' de C et AA' de C'.
Tracer la droite
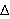passant par A et parallèle à (BD). Cette droite est sécante
à (BC) en E et à (CD) en F. Déterminer la nature du triangle
ECF.
Construire un triangle rectangle isocèle ABC tel que AB = BC = 4 cm. Construire un triangle rectangle isocèle CDE, rectangle en D, tel que :
Le point D est le symétrique du point B par rapport au point C.
Les points A et E sont du même côté de la droite (BD).
Démontrer que les segments [AD] et [BE] se coupent en leur milieu. Soit I ce point.
Soit F le point d'intersection des segments [AD] et [CE] ; montrer que FE = 2 CF.
Comparer, sans calculer, les aires des triangles ACF et DEF.
Calculer l'aire du triangle ACF.
En utilisant uniquement la règle graduée et le compas, construire la figure suivante :
ABCD est un rectangle tel que AB = 8 cm et AD = 6 cm.
BDEF est un rectangle tel que A soit un point de [EF].
O est le point d'intersection des diagonales du rectangle ABCD.
H est le point de [EF] tel que la droite (OH) soit parallèle à la droite (AD).
Calculer BD.
Calculer l'aire du triangle ABD. En déduire la valeur de ED et comparer les aires de BDEF et ABCD.
Montrer que AHOD est un parallélogramme. Que peut-on dire du quadrilatère AHBO ?
Soient (DA) et (D'A) deux droites sécantes en A, telles que D'A
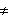DA. Tracer le cercle (C) de diamètre [DA] et le cercle (C') de
diamètre [D'A]. (C) et (C') se coupent en A et en B. On note O et O'
leurs centres respectifs. (DA) recoupe (C') en E' et (D'A) recoupe (C) en
E.
Que pouvez-vous dire des droites (DE) et (EA) ? des droites (D'E') et (E'A) ? Justifiez.
Les droites (DE) et (D'E') se coupent en F. Que représente le point A pour le triangle FDD' ? Justifiez.
Démontrez que les droites (AB) et (DD') sont perpendiculaires.
Montrer que les points A, B et F sont alignés.
En déduire que les droites (DE), (BA) et (D'E') sont concourantes.
Soit un cercle (C) de centre O et de rayon 4cm, [AB] un diamètre de ce cercle et D un point du cercle tel que AD = 4 cm.
Quelle est la nature du triangle AOD ? Justifier.
Quelle est la nature du triangle ABD ? Justifier.
Soit H le milieu de [BD]. Montrer que la droite (OH) est parallèle à la droite(AD).
Le point I désignant le milieu du segment [AO], la droite (DI) recoupe le cercle (C) en E. Démontrer que le quadrilatère DAEO est un losange, puis que les points E, H et O sont alignés.
Démontrer que la droite (DO) est perpendiculaire à la droite (BE).
Soient A et B deux points tels que AB = 10 cm.
Déterminer tous les points C vérifiant simultanément les deux conditions :
On considère un angle droit xOy. Un point E se déplace sur la demi-droite [Ox), un point F se déplace sur la demi-droite [Oy) de telle sorte que EF reste toujours égal à 10 cm. Soit M le milieu de [EF].
1. Quel est l'ensemble décrit par le point M quand E et F prennent toutes les positions possibles ?
2. Calculer la longueur de la hauteur OH du triangle EOF dans le cas où EO = 8 cm et OF = 6 cm.
Soit un cercle C de centre O et de rayon 4 cm.
1. Donnez un programme de construction, à la règle non graduée et au compas, d'un hexagone régulier ABCDEF inscrit dans ce cercle. Réalisez ce programme.
2. Démontrez que la droite (AC) est la médiatrice du segment [BO] et que la droite (BO) est la médiatrice du segment [AC].
3. Démontrez que les points A et D sont diamétralement opposés.
4. Quelle est la nature du quadrilatère ACDF ? Justifiez votre réponse.
5. Calculez l'aire de ce quadrilatère.
6. Les segments [AC] et [BF] se coupent en I. Démontrez que A et B sont symétriques par rapport à la droite (OI) et que C et F sont symétriques par rapport à la droite (OI).
On donne un hexagone régulier convexe ABCDEF. Soit I le point d'intersection des droites (AF) et (BC), J le point d'intersection des droites (ED) et (BC), K le point d'intersection des points (ED) et (AF).
1. Montrer que le triangle IJK est équilatéral.
2. Calculer la valeur du rapport : aire de IJK / aire de ABCDEF
Dans cet exercice, tous les ensembles trouvés seront tracés
sur une même figure.\\
Soient A et B deux points distincts du plan.\\
Quel est l'ensemble des points M du plan tels que :
ABM soit un triangle rectangle en A ou en B ?
ABM soit un triangle rectangle en M ?
ABM soit un triangle isocèle en A ou en B ?
ABM soit un triangle isocèle en M ?