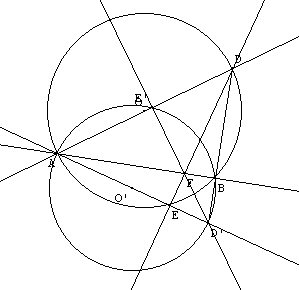
- Le triangle AED est inscrit dans un demi-cercle de diamètre AD, donc il est rectangle. Donc les droites (AE) et (DE) sont perpendiculaires. Il en va de même des droites (AE') et (E'D) dans l'autre cercle.
- D'après la question précédente, (D'E') est perpendiculaire à (DE), donc (DE) est la hauteur issue de D dans le triangle DFD'. De même, (DF) est perpendiculaire à (D'E), donc (D'E) est la hauteur issue de D'. A est l'intersection de deux hauteurs du triangle DFD', donc A est l'orthocentre du triangle FDD'.
- (AB) est perpendiculaire à (DD') car le triangle ABD' est inscrit dans un demi-cercle de diamètre AD'.
- (AF) est la troisième hauteur de FDD'. Donc (AF) est perpendiculaire à (DD'). Donc (AF) et (AB) sont perpendiculaires à (DD'), donc ces deux droites sont confondues. Donc A, F et B sont alignés.
- (DE), (BA) et (D'E') sont les trois hauteurs de ADD', elles sont donc concourantes. F est l'orthocentre de ADD'.