| 1.
AI = AB/2 et AJ = AD/2. Or AB=AD car ABCD est un carré.
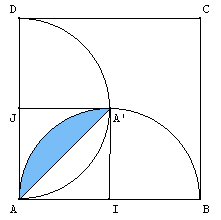
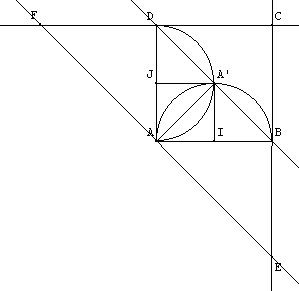
Donc AI=AJ. Or IA’=IA, comme rayons du même cercle, et de même JA’=JA. Donc AI=AJ=IA’=JA’. Donc AIA’J est un losange, comme l’angle de sommet A est droit, c’est un carré. |
 |
| 2.
Considérons la zone délimitée par le segment [AA’] et l’un des
deux arcs AA’. Son aire est la moitié de l’aire cherchée.
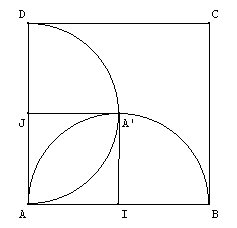
Cette zone est obtenue en retranchant un demi carré de côté 3 à un quart de disque de rayon 3. L’aire cherchée s’obtient donc en effectuant le calcul : 2*(pi*9/4-9/2) = 9pi/2-9 soit environ 5,13 cm². |
 |
| 3. Le triangle ECF est rectangle car l’angle C est droit. Le théorème de Thalès (ou celui de la droite des milieux) appliqué aux droites sécantes (CD) et (CB) et aux droites parallèles (BD) et D permet d’écrire : CE/CB = CF/CD. Or CB=CD, donc CE=CF. Le triangle ECF est donc isocèle rectangle. |  |