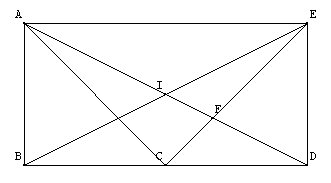

1. Les triangles ABC et CDE sont rectangles, et B, C, D sont alignés. Donc les droites (DE) et (AB) sont perpendiculaires à (BD) et donc parallèles entre elles. AB=DE et le quadrilatère ABDE n’est pas croisé, donc ABDE est un parallélogramme, donc ses diagonales se coupent en leur milieu.
2. Considérons le triangle EBD. Les droites (EC) et (DI) sont des médianes de ce triangle. Leur point d’intersection F est donc le centre de gravité, on sait qu’il est situé sur chaque médiane aux deux tiers de la longueur à partir du sommet. Donc FE = 2CF.
3. Les triangles ACD et ECD ont la même aire car ils ont la même base et la même hauteur. Si on leur retranche le triangle CDF, on obtient deux triangles de même aire : ACF et EFD.
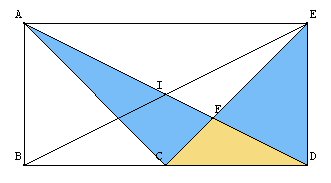
4. L’aire du triangle ACF est égale à l’aire du triangle EFD. Or le triangle EFD a pour base [EF] et pour hauteur [DH] (H projeté orthogonal de D sur (CE)). Le triangle CDE a pour base [CE] et pour hauteur [DH]. Comme FE= 2/3CE, l’aire de CFD est égale aux deux tiers de celle de CDE. L’aire de CDE s’obtient par : CD*DE/2= 8 cm². Donc l’aire de ACF vaut 16/3 cm².