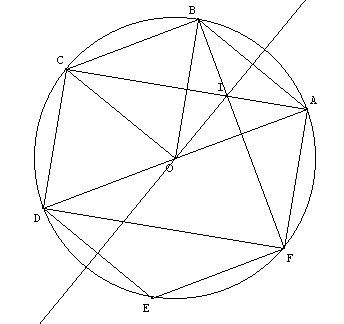
2.      L’hexagone régulier est constitué de six triangles équilatéraux. Donc CO=CB et OA=AB donc (AC) est la médiatrice de [BO]. De même OA=OC et AB=BC, donc (OB) est la médiatrice de [AC].

3.      Utiliser les angles de 60° pour montrer que l'angle est plat.

4.      On montre de même qu’au dessus que F, O et C sont alignés et que O est le milieu de [FC]. Donc ACDF est un parallélogramme. On montre que les diagonales ont la même longueur ; ACDF est donc un rectangle.

5.      Avec le théorème de Pythagore, on calcule AC=2rac(3), d’où l’aire de 8rac(3).

6.      (BF) et (AC) sont des médianes –médiatrices de OAB, donc I est le centre de gravité de OAB. (OI) est donc l’axe de symétrie de [AB]. (AC) et (BF) sont symétriques par rapport à (OI) et OC=CF donc C et F sont symétriques par rapport à (OI).