|
1. 2x – 1 = ¾ |
4. x /4 – 1 = ½ |
6. |
|
2. 3x – 1 = 6x + 3 |
5. |
7. |
|
3. 3 – x = 4(x – 5) |
|
|
Un père a le triple de l'âge de son fils. Dans onze ans, l'âge du père sera le double de celui du fils. Quels sont les âges respectifs du père et du fils ?
Trouver trois nombres dont la somme est 22, tels que le premier soit le double du second et le triple du troisième.
Trois magasins vendent les mêmes tablettes de chocolat.
Au magasin A, on les vend à l'unité : 6,50 F.
Au magasin B, on les vend par lots de deux : 12,50 F le lot.
Au magasin C, on les vend
On accepte de s'approvisionner dans plusieurs de ces magasins, s'il le faut; Quelle est alors la solution la plus avantageuse pour acheter 6, 7, ou n tablettes
Un marchand participe à trois foires, il vend puis il achète.
A la première, il double la somme d'argent dont il dispose et dépense 30 écus.
A la seconde, il triple la somme d'argent dont il dispose et dépense 54 écus.
A la troisième, il quadruple la somme d'argent dont il dispose et dépense 72 écus.
Il lui reste alors 48 écus.
Combien avait-il d'argent au départ ?
(note: on suppose qu'il dispose au début de chaque foire de l'argent lui restant après la foire précédente)
Un nombre est écrit avec trois chiffres. Si l'on échange le premier et le troisième chiffre, le nombre diminue de 198. Le chiffre du milieu est un 5 et le nombre est un multiple de 9.Calculer ce nombre.
Choisissez trois entiers consécutifs. Calculez le produit du premier par le troisième. Calculez le carré du deuxième. Que remarquez-vous ?
Trouverez-vous ce résultat quels que soient les trois entiers consécutifs choisis ? Expliquer.
Dans quatre ans, je serai trois fois plus âgé que ma fille. Il y a deux ans, j'étais cinq fois plus âgé qu'elle. Quel est mon âge ? Quel est l'âge de ma fille ?
Un écolier a en sa possession 120 billes. Il dit à un de ses camarades : "Je pense à un nombre sans te dire lequel. Si je te donne 5 fois ce nombre de billes, il m'en restera au moins 20 sur les 120 que je possède. Si par contre tu m'en donnes 4 fois ce nombre, j'en aurai au moins 200.
Résoudre les équations suivantes :
|
1. 2x – 1 = ¾ |
4. x /4 – 1 = ½ |
6. |
|
2. 3x – 1 = 6x + 3 |
5. |
7. |
|
3. 3 – x = 4(x – 5) |
|
|
Résoudre les équations suivantes :
|
1. (5x – 3)(2 – 3x) = 0 |
2. 3x (2x – 7) = 0 |
3. (-3x + 1)² = 0 |
4. x² (-3 – 2x) = 0 |
Dans chaque cas, factoriser le membre de gauche afin de se ramener à une équation produit, puis la résoudre.
|
1. (x – 2)(2x + 1) + 3(2x + 1) = 0 |
4. 3 (x – 1)² + 4x – 4 = 0 |
|
2. (5x + 1)² - 2x (5x + 1) = 0 |
5. Résoudre chacune des équations suivantes : (x + 3)² = 4 (x – 5)(x + 5) = x² + 7x + 3 |
|
3. (2x + 3)² - (x – 2)² = 0 |
Trouver trois entiers consécutifs dont la somme est comprise entre 2 999 et 3 001.
1. Trouver trois entiers consécutifs dont la somme vaut 2 001.
2. Si l’on diminue la longueur du côté d’un carré de 2 cm, son aire diminue de 52 cm². Quelle est la longueur initiale du côté du carré ?
3. Les superficies de deux jardins carrés diffèrent de 136 m². Le côté du plus grand mesure 4 m de plus que le côté de l’autre. Calculer la surface de chaque jardin.
4. La location d’un autocar pour une sortie touristique revient à 11€ par touriste inscrit. Il y a 4 désistements et chaque participant a dû régler 13€. Que était le nombre de touristes initialement inscrits ?
5. Deux villes M et C sont distantes de 110 km. Une voiture part de M et se dirige vers C à la vitesse de 90 km/h, une autre voiture part de C et se dirige vers M à la vitesse de 75 km/h. A quelle distance de M aura lieu le croisement ? Au bout de combien de temps après leur départ, les voitures se sont-elles croisées ?
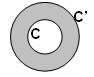
C et C’ sont deux cercles concentriques, le rayon de C’ étant plus grand de 2 mètres que celui de C.
Déterminer le rayon du cercle C pour que l’aire de la couronne grisée ci-dessous soit inférieure à 100 m².
Une entreprise de confection propose à ses couturières deux types de contrats :
Contrat A : salaire mensuel fixe de 320 € auquel s’ajoutent 26 € par vêtement réalisé ;
Contrat B : salaire mensuel fixe de 686 € et 8 € par vêtement réalisé.
Déterminer, suivant le nombre de vêtements réalisés, le contrat le plus avantageux pour la couturière.