Géométrie dans l'espace
retour page
d'accueil
Soit ABCDEFGH un
parallélépipède rectangle tel que :
- AB = CD =
EF = GH = 8 cm
- AD = BC = EH = FG = 6
cm
- AE = BF = CG = DH = 4
cm
1.
Représenter le solide en
perspective cavalière : on placera la face ABCD en plan frontal, on utilisera un
coefficient de réduction de 0,5 sur des fuyantes à 45°.
2.
Calculer la longueur de la
diagonale [AG].
3.
Soit M le point de [EF] tel que
MF = 2 cm. Une fourmi désire se rendre de M en C par le chemin le plus court en
restant à la surface du parallélépipède. Quelle est la longueur de ce chemin ?
Soit ABCDEFGH un cube de 6
cm de côté.
Représenter le cube en
perspective cavalière, la face ABCD étant « sur le sol » et la face ABFE étant
située dans le plan frontal.
Soient I, J, K, L, M, N, O,
P, Q, R, S, T les milieux respectifs des arêtes [AB], [BC], [CD], [DA], [EF], [FG],
[GH], [HE], [BF], [GC], [HD] et [EA].
On réalise un solide S en
retirant au cube les tétraèdres BQIJ, GONR, PMTE et LKSD.
Réaliser un patron du solide
S et construire le solide en taille réelle.
Quel est le volume de S ?
Soit un cube
ABCDEFGH d’arête 5 cm. Soit S le point de l’arête [EF] situé à 2 cm de F.
Construire en
vraie grandeur un patron de la pyramide à base carrée SABCD.
ABCD est un tétraèdre
régulier d’arête 6 cm. On enlève à ce solide, aux quatre sommets A, B, C, D
quatre tétraèdres T1, T2, T3, T4 identiques : T1 est le tétraèdre de sommets A,
E, F, G où E est sur [AB], F sur [AC], G sur [AD] et AE = AF = AG = 2 cm. T2,
T3 et T4 sont définis de lanière analogue.
1.
Décrire le solide obtenu en
justifiant les réponses.
2.
Construire un modèle de chaque
face en respectant les dimensions et en décrivant vos constructions.
3.
Tracer un patron du solide en respectant les dimensions.
|
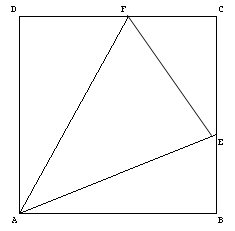
Soit ABCD un carré de côté 4 cm. Où les points E et F doivent-ils être
placés respectivement sur [BC] et sur [CD] pour que la figure ci-contre
soit un patron de pyramide ?
1.
Quelle est alors la
nature de chacune des faces de cette pyramide ?
Soit K le sommet du solide où se rejoignent les points B, C et D du
patron. On obtient la pyramide (le tétraèdre) AEFK.
2.
Montrer que l’on peut
faire coïncider AEFK avec le coin d’un cube de 4 cm de côté. Représenter
ce cube en perspective et y tracer une représentation de la pyramide.
3.
Calculer le volume de
AEFK.
4.
Calculer l’aire du
triangle AEF.
5.
Soit K' le projeté
orthogonal de K sur le plan (AEF). Calculer KH.
|
 |
