Pour obtenir un patron de pyramide il faut que les segments [BE] et [EC] d'une part, [FD] et [FC] d'autre part, soient de même longueur. Il faut donc que E et F soient les milieux de [BC] et [CD].
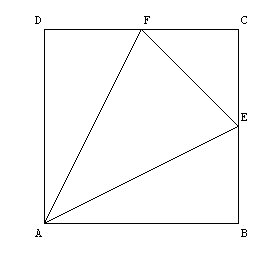
1. Le triangle CFE est rectangle isocèle, les triangles DFA et AEB sont rectangles (et isométriques). On peut calculer AF et AE en utilisant le théorème de Pythagore dans les triangles rectangles ADF et ABE, on obtient : AE=AF=rac(20).
|
2. On peut placer les trois faces qui sont des triangles rectangles au sommet d'un cube dont l'arète mesure 4 cm. Les points E et F sont alors les milieux de deux arètes, K et A sont des sommets du cube. 3. Le volume de AEFK s'obtient en multipliant la mesure de l'aire de la base FKE par la hauteur AK et en divisant par 3. On a donc : V(AEFK)=((2*2/2)*4)/3=8/3 cm3 4. On peut calculer l'aire du triangle AEF en
utilisant le théorème de Pythagore pour déterminer sa hauteur et
sa base, mais il est plus simple de revenir à la figure initiale
: l'aire de AEF est l'aire du carré ABCD privé des trois
triangles rectangles ABE, ADF et EFC. 5. Le volume de AEFK peu aussi s'obtenir en multipliant l'aire de AEF par la distance KK' de K à cette face et en divisant par 3. On a donc 6KK'=8/3. Donc KK'=4/9 cm.
|
 |