1 .
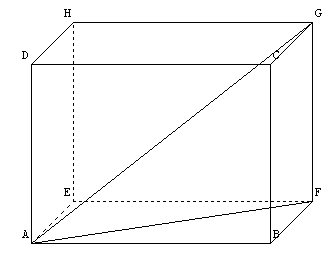
AF²=AB²+BF² donc AF²=64+16=80. Donc AF=rac(80)
(FG) est perpendiculaire au plan (ABFE), donc à la droite (AF). Le triangle AFG est donc rectangle.
On applique encore le théorème de Pythagore : AG²=AF²+GF² donc AG²=80+36=116 et AG=rac(116)
3. Il faut trouver où placer le point N sur [FG], ou le poin P sur [GH] ou le point Q sur [AB] afin d'obtenir un trajet minimal.
Pour cela "déplions" le patron du parallélépipède dans chacun des trois cas
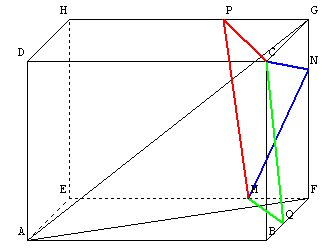
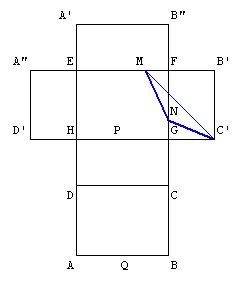
Le chemin MNC est minimal si ces trois points sont
alignés.
On obtient alors, avec le théorème de Pythagore dans le triangle MB'C' :
MC'²=36+36=72 donc MC'=rac(72)

Même raisonnement : le chemin MPC est minimal quand les trois points sont alignés.
Dans le triangle rectangle MFC on a :
MC²=4+100=104 donc MC=rac(104)
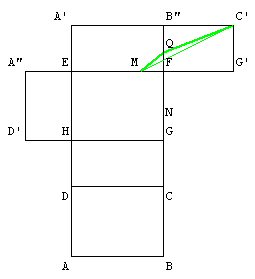
De même, en changeant de patron :
Dans le triangle MG'C', MC'²=16+64=80
donc MC'=rac(80)
Le parcours le plus court est donc le premier, il mesure rac(72).