1.
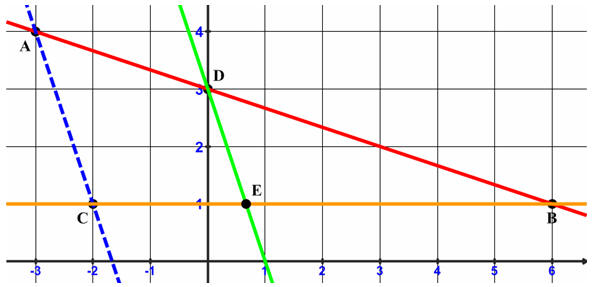
On commence par déterminer une équation de la droite (AB) : elle est de
la forme y = m x + p, avec m < 0 puisque le droite (AB) est décroissante.
.
Comme la droite passe par A, les coordonnées de ce point vérifient l’équation de
la droite : d’où 4 = 
´(-3)
+ p, c’est-à-dire p = 3.
(AB) a pour équation y = x
+ 3.
Le point D appartient à la droite (AB) ssi ses coordonnées vérifient son équation, ce qui est le cas.
2.
Deux droites parallèles ont même coefficient directeur ; donc celui de la
droite (DE) est -3. De plus l’ordonnée à l’origine de la droite (DE) est 3 ; son
équation est donc
y = -3x + 3. Les points C et B ayant la même ordonnée 1, la droite
(CB) a pour équation
y = 1.
Le point E est l’intersection des droites (DE) et (CB) ;
ses coordonnées vérifient donc le système de deux équations à deux inconnues
,
qui sont (2/3 ; 1).
