Comme x désigne la longueur du rectangle et h sa largeur, nécessairement le périmètre, égal à 40 cm, est aussi égal à 2(x + h) ;
on obtient donc la relation 2(x + h ) = 40 d’où l’on tire l’autre relation h = 20 – x.
L’aire du rectangle, notée f(x), s’obtient en faisant le produit de la longueur par la largeur ; ainsi :
f(x) = x ´ h = x ´(20 – x) = 20x – x². f(x) = 20x – x²
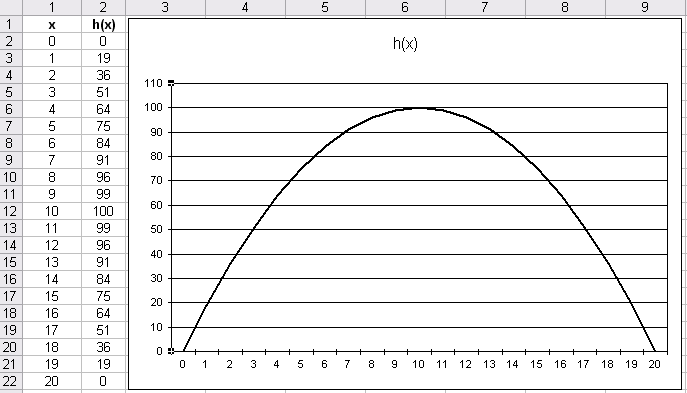
A l’aide d’un tableur, on construit la courbe représentative de la fonction f sur l’intervalle [0 ; 20] (0 et 20 sont les solutions de l’équations f(x) = 0 et on ne considère que les valeurs positives de x étant donné que les dimensions du rectangle doivent être positives !).
La courbe représente un arc de parabole, dont le maximum 100 est atteint en x = 10.
Ainsi l’aire du rectangle est maximale lorsque longueur et largeur mesurent 10 cm, c’est-à-dire lorsque le rectangle a la forme particulière du carré.
