télécharger le document au format pdf
| -3000 à -500 | La géométrie est purement utilitaire (calculs d'aires, de distances, architecture..), on ne s'intéresse pas du tout à l'aspect démonstration. |
| Vème et IVème siècles av. JC | Pythagore, Aristote : la géométrie fait partie de la philosophie, c'est une clé pour comprendre le monde. Apparition de la démonstration, élément du dialogue philosophique (ex. la maïeutique de Socrate ; Euclide rassemble les résultats connus dans ses "Eléments". ) |
| Xème siècle ap. JC | Trigonométrie (mathématiciens arabes) |
| XVIème siècle | Géométrie projective (Girard Desargues) |
| XVIIème siècle | Géométrie analytique (Descartes) : invention des coordonné es. |
| XVIIIème siècle | Géométrie descriptive (Monge) |
| XIXème siècle | Invention des géométries non euclidiennes (Lobachevski et Riemann) |
| XXè me siècle | Une géométrie est un ensemble de transformation sur un ensemble d'objets avec un ensemble de règles. |
| angle | portion du plan délimitée par deux demi-droites de même origine. |
| angle droit | angle dont les côtés sont perpendiculaires |
| angle aigu | angle plus petit qu'un angle droit. |
| angle obtus | angle plus grand qu'un angle droit |
| angle plat | angle double d'un angle droit |
| angle rentrant | angle plus grand qu'un angle plat |
| angle saillant | angle plus petit qu'un angle plat |
| angles complémentaires | angles dont la somme des mesures équivaut à celle d'un angle droit |
| angles supplémentaires | angles dont la somme des mesures équivaut à celle d'un angle plat |
| cercle | le cercle de centre O et de rayon r est l'ensemble des points situés à la distance r de O. |
| disque | ensemble des points situés à l'intérieur d'un cercle |
| corde | segment dont les extrémités appartiennent au cercle |
| diamètre | corde passant par le centre |
| arc | portion de cercle délimitée par deux points |
| tangente | droite ayant exactement un point de contact avec un cercle, en ce point la tangente est perpendiculaire au rayon |
| rayon | segment dont les extrémités sont le centre du cercle et un point du cercle |
| angles complémentaires | angles dont la somme des mesures équivaut à celle d'un angle droit |
| angles supplémentaires | angles dont la somme des mesures équivaut à celle d'un angle plat |
| triangle | polygone de trois côtés. |
| triangle acutangle | triangle dont tous les angles sont aigus |
| triangle équilatéral | triangle ayant ses trois côtés de même longueur |
| triangle isocèle | triangle ayant deux côtés de même longueur |
| triangle rectangle | triangle ayant un angle droit |
| triangle scalène | triangle n'étant ni rectangle ni isocèle |
| hypoténuse | le plus grand côté d'un triangle rectangle (les petits s'appellent des "cathètes") |
| polygone | ligne brisée fermée |
| polygone convexe | polygone tel que tout segment joignant des points intérieurs est intérieur au polygone |
| polygone concave | polygone non convexe |
| polygone croisé | polygone dont deux côtés sont sécants |
| polygone régulier | polygone dont tous les angles au sommet sont de même mesure et dont tous les côtés sont de même longueur |
| quadrilatère | polygone à quatre côtés |
| penta-, hexa-, hepta-, octo-, ennea-, déca-, endéca, dodéca...gone | polygone à 5, 6, 7, 8, 9, 10, 11, 12 ... côtés. |
|
Un site illustré et intéressant : http://www.automaths.com/construction/construction.htm |
Pour tracer un triangle équilatéral ABC : tracer un segment [AB], prendre au compas l'ouverture AB. Pointer successivement en A et en B, tracer deux arcs de cercle sécants en C. Tracer les segments [AC] et [BC].
Soit
un angle. Pointer le compas en O, tracer un arc de cercle coupant les deux
côtés de l'angle en A et en B. Avec une ouverture quelconque pointer
en A puis en B et tracer deux arcs de cercles sécants en un point C. La
bissectrice est la demi-droite [OC).
Soit [AB] un segment. Prendre une ouverture de compas supérieure à la moitié de AB, pointer successivement en A et en B et tracer deux grands arcs de cercles sécants en deux points C et D. (CD) est la médiatrice de [AB]. L'intersection de [AB] et de (CD) est donc le milieu de [AB].
60°,
30° ...Pour tracer un angle de 60° tracer un triangle équilatéral. Pour tracer un angle de 30°, tracer un angle de 60° puis sa bissectrice ...
Pour tracer la perpendiculaire à une droite
D
passant par un point A, pointer le compas en A, prendre une ouverture assez
grande pour tracer un arc coupant
D
en deux points B et C, puis tracer la bissectrice de [BC].
Pour tracer la parallèle à une droite
D
passant par un point A, tracer la perpendiculaire, puis la perpendiculaire
à la perpendiculaire. ou Prendre une ouverture de compas assez grande
pour tracer un arc coupant
D
en deux points B et C, puis tracer un parallélogramme ABCD en reportant
la longueur BC à partir de A et la longueur AB à partir de C.
 |
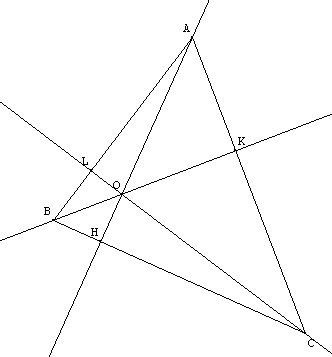On appelle hauteur du triangle toute droite perpendiculaire à un
côté et passant par le sommet opposé. Les trois hauteurs se
coupent en un même point (elles sont "concourantes") appelé
l'orthocentre du triangle.
Si le triangle est acutangle, l'orthocentre est à l'intérieur du triangle, si le triangle est obtusangle, l'orthocentre est extérieur au triangle, si le triangle est rectangle, l'orthocentre est le sommet de l'angle droit. |
 |
|
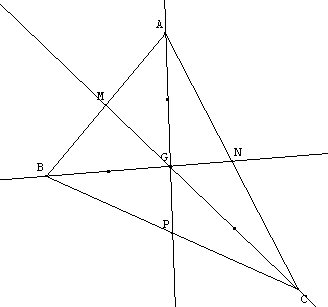
On appelle médiane du triangle toute droite passant par un sommet et le milieu du côté opposé.
Les trois médianes se coupent en un même point appelé le centre
de gravité du triangle. Le centre de gravité partage les segments
des médianesintérieurs au rectangle dans un rapport de
|
 |
|
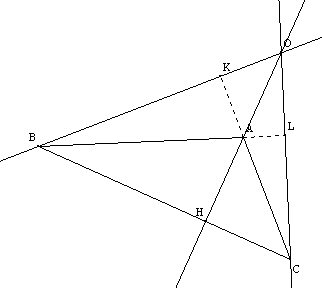
Les trois médiatrices des côtés du triangle se coupent en un même point appelé le centre de cercle circonscrit au triangle.
|
 |
|
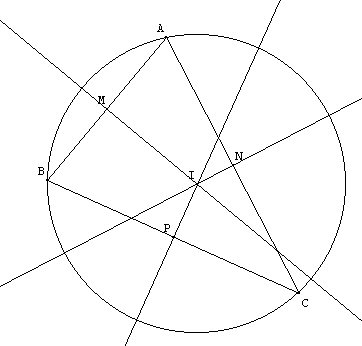
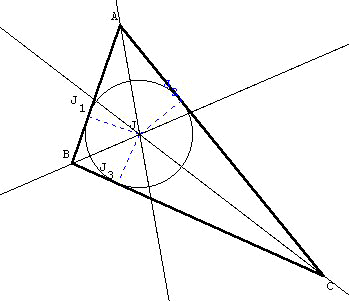
Les trois bissectrices des angles du triangle se coupent en un même point appelé le centre de cercle inscrit au triangle. |
 |
Un quadrilatère convexe est un trapèze s'il a deux côtés parallèles. Si de plus il a un axe de symétrie, c'est un trapèze isocèle. S'il a un angle droit, le trapèze est dit trapèze rectangle.
Un quadrilatère est un parallélogramme si l'une des caractérisations suivantes est vérifiée :
- ses côtés sont parallèles deux à deux
- ses côtés opposés sont égaux deux à deux
- ses diagonales se coupent en leur milieu
- le quadrilatère n'est pas croisé et deux côtés opposés sont parallèles et de même longueur (égalité des vecteurs).
Un quadrilatère est un losange si l'une des caractérisations suivantes est vérifiée :
ses côtés de même longueur
c'est un parallélogramme et ses diagonales sont perpendiculaires
c'est un parallélogramme et deux côtés consécutifs sont de même longueur
Un quadrilatère est un rectangle si l'une des caractérisations suivantes est vérifiée :
il a trois angles droits
c'est un parallélogramme et ses diagonales sont de même longueur
c'est un parallélogramme et deux côtés sont perpendiculaires
Un quadrilatère est un carré si l'une des caractérisations suivantes est vérifiée :
c'est un losange et il a un angle droit
c'est un rectangle et ses diagonales sont perpendiculaires
Si
ABC
est un triangle rectangle en
A,
on a :
.
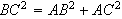Si, dans un triangle
ABC,
,
alors
ABC
n'est pas rectangle en
A.
Si dans un triangle ABC, on a
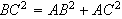, alors ABC est rectangle en A.
Premier énoncé
Si ABC est un triangle, M le milieu de [AB] et N le milieu de [AC], on a : (MN) // (BC) et BC = 2 MN. |
|
Deuxième énoncé
Si ABC est un triangle, M le milieu de [AB] et D la droite parallèle à (BC) passant par M, alors D coupe [AC] en son milieu. |
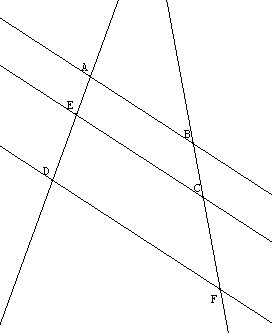
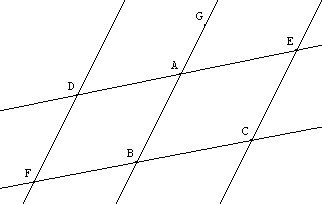
Si
D
On a ainsi AE/AD = BC/BF
|
 |
 |
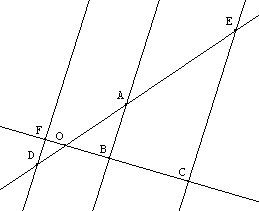dans une situation "en triangle" ou "en papillon", on a aussi l'égalité des rapports pour le troisième côté. On a ici : OA/OE=OB/OC=AB/EC et OA/OD=OB/OF=AB/DF
|
cas général
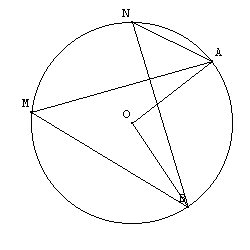
Soit
Le cas du triangle rectangle
Si
[
|
 |
 |
|
